Capítulo 10 Estimación por intervalo

Hemos llegado a este punto en el que haremos uso de casi todos los elementos que se presentaron hasta aquí. Se dedicó la Parte I a la descripción de datos provenientes de una muestra y luego, en la Parte II se ingresó al terreno de la incertidumbre. Solo resta integrar estos elementos en un procedimiento para realizar las estimaciones que interesen. Por esta razón éste es un capítulo de plena aplicación práctica.

10.1 Estimación puntual

La media muestral \(\overline{x}\) es un estimador de la media poblacional, así como la proporción muestral (\(\widehat{p})\) estima a la proporción poblacional (\(P\)), a estas estimaciones se las llama estimaciones puntuales, porque ofrecen un único valor como estimación del parámetro de interés. Por ejemplo si en una muestra de 50 personas que egresaron de una carrera universitaria en los últimos diez años se encuentra que han terminado la carrera con una nota promedio de \(\overline{x} = 6.50\), disponemos de una media muestral; si ahora preguntamos por el promedio con que terminan la carrera todas las personas que egresan, la respuesta es tentativa, porque la población es hipotética, en el futuro seguirá habiendo nuevos egresos. Diremos que posiblemente es cercano a 6.50”. Con esta expresión imprecisa, hacemos una estimación de la media poblacional (\(\mu\)). De igual modo, si en la misma muestra de 50 profesionales, se ve que la proporción de mujeres es \(\widehat{p} = 0.70\), podremos decir que, del total de quienes se reciben en esa carrera, alrededor del 70% son mujeres. Así hacemos una estimación de \(P\) a partir de \(\widehat{p}\). Pero estas estimaciones son deficientes, ya que no sabemos cuán cerca puede estar la verdadera nota promedio de 6.50 ó la verdadera proporción de mujeres del 70%. Estas son las que se denominan estimaciones puntuales.

La Encuesta Permanente de Hogares de Argentina da para el aglomerado Gran Córdoba, en el tercer trimestre de 2018, un ingreso salarial promedio, para los varones, de

## [1] 16860.5

Este es el resultado descriptivo que corresponde a los 402 asalariados varones fueron encuestados en ese aglomerado y declararon sus ingresos salariales. El ingreso salarial promedio de todos los trabajadores en relación de dependencia es un valor desconocido, que es probable que sea cercano al que se halló en la muestra, pero no puede asegurarse.

La encuesta Latinobarómetro 2017 da la siguiente distribución de frecuencias para las respuestas dadas a la pregunta si cree que se puede o no confiar en la gente.

Hablando en general, ¿Diría Ud. que…	\(f\)
Se puede confiar en la mayoría de las personas	2833
Uno nunca es lo suficientemente cuidadoso en el trato con los demás	16915
Sum	19748

La proporción de quienes creen que se puede confiar en la mayoría de las personas es \(\widehat{p}=\frac{2833}{19748}= 0.142\). De esto se puede leer que el 14.2% de las personas encuestadas responde de esa manera, pero la generalización a la población de donde la muestra fue extraída solo puede hacerse de manera tentativa: alrededor del 14.2% del total opina que se puede confiar en la mayoría de las personas.

Así. la generalización a la población no es la simple transferencia del valor muestral a un conjunto más grande. Como vimos en el capítulo anterior, las leyes que relacionan la muestra y la población son probabilísticas; esas leyes son las que hay que usar para hacer la inferencia desde la muestra hacia la población.

10.2 Intervalos de confianza

Una estimación más completa de los parámetros mencionados, se denomina estimación por intervalo. Ella consiste en ofrecer no ya un número como en la estimación puntual, sino un intervalo, acerca del cual se tiene cierto grado de certidumbre (o se deposita cierta confianza) que contenga al parámetro. Así, en lugar de decir que el promedio con que egresan quienes terminan una carrera universitaria “debe ser cercano a 6.50”, se construirá un intervalo, que dirá, por ejemplo, “hay una confianza del 95% en que el intervalo \([6.10; 6.90]\) contiene al promedio con que se termina esa carrera”. De manera equivalente, en lugar de “entre quienes egresan hay alrededor del 70% de mujeres”, se afirmará algo como “con una confianza del 95%, el intervalo \([68; 72]\)% contiene a la proporción de mujeres sobre el total quienes egresan”. O que “con una confianza del 95%, el ingreso salarial promedio de los trabajadores del aglomerado Gran Córdoba está entre \(16710.5\) y \(17010.5\). Y también que en la población mayor de 18 años residente en países de América Latina, hay una confianza de 90% que la propoción de quienes creen que se puede confiar en la mayoría de la gente, esté en el intervalo \([14.20, 14.49]\)%.

Vemos entonces que esta forma de estimar ofrece dos números, los límites de un intervalo, del que esperamos contenga al parámetro que estimamos. Decimos “esperamos que se contenga” porque no hay certeza absoluta de que se encuentre allí, hay una confianza que en estos ejemplos hemos fijado en el \(95\)% o en \(90\)%, y veremos que puede elegirse.

Veamos a continuación cómo construir estos intervalos de confianza para estimar los dos primeros parámetros que hemos tratado; la media y la proporción.

10.3 Estimación de la media

Vamos a hacer uso de lo que sabemos hasta el momento sobre las distribuciones en el muestreo para mejorar la calidad de las estimaciones puntuales y construir los intervalos de confianza. Para ello, empezaremos con la media. Debido a que la muestra ha sido obtenida de manera aleatoria, la media muestral es una variable aleatoria, cuya distribución tiene media \(\mu\) y desviación estándar \(\sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}}\). Además, a medida que aumenta el tamaño de la muestra, esa distribución tiende a ser normal, es decir que será tanto más cercana a una distribución normal cuanto más grande sea \(n\). A los fines prácticos, una muestra de 30 casos se considera “suficientemente grande” como para usar la distribución normal en la distribución de \(\overline{x}\). Si la muestra es más pequeña que ese tamaño, no podemos usar inmediatamente la distribución normal, sino que deberemos apelar a la distribución t de Student. Trabajaremos primero suponiendo que se trata de muestras lo suficientemente grandes y usaremos la distribución normal. Los paquetes informáticos de análisis de datos usan la distribución t siempre, cualquiera sea el tamaño de la muestra, haciendo uso de la convergencia de esta distribución hacia la normal cuando \(n\) crece.

Con esa información, podemos calcular las probabilidades de los diferentes valores de \(\overline{x}\). La representación gráfica de esta distribución es la de la figura 10.1:

Figura 10.1: Distribución de las medias muestrales

Ya sabemos que una variable que tenga distribución normal tiene probabilidad 0.95 de tomar un valor que diste menos de \(1.96\) desviaciones estándar de la media. Eso mismo, dicho en términos frecuenciales implica que, bajo el modelo normal, el 95% de los casos se encuentra entre 1.96 desviacioens estándar por debajo y 1.96 desviaciones estándar por encima de la media. Por lo cual, si extrajéramos todas las muestras de tamaño \(n\) posibles de esa población, el 95% de ellas estaría entre \(\mu - 1.96*\sigma_{\overline{x}}\) y \(\mu + 1.96*\sigma_{\overline{x}}\), o lo que es lo mismo, entre \(\mu - 1.96*\frac{\sigma}{\sqrt{n}}\) y \(\mu + 1.96*\frac{\sigma}{\sqrt{n}}\).

Figura 10.2: Intervalo en torno a la media poblacional que incluye al 95% de las posibles medias muestrales

De manera equivalente, como a 2.57 desviaciones estándar alrededor de la media se encuentra el 99% de las observaciones, entonces el 99% de las medias muestrales estará entre \(\mu - 2.57*\frac{\sigma}{\sqrt{n}}\) y \(\mu + 2.57*\frac{\sigma}{\sqrt{n}}\).

Figura 10.3: Intervalo en torno a la media poblacional que incluye al 99% de las posibles medias muestrales

Este es el alcance más operativo de los resultados teóricos, ahora hay que ir al problema práctico. Las curvas de arriba solo pueden dibujarse si se conoce \(\mu\) y es justamente el valor que trata de estimarse. Además, en el muestreo no se extraen “todas las muestras” sino solo una, y ella se usa para hacer la estimación. Lo que sabemos de esa muestra es que tiene una probabilidad del \(0.95\) de estar en la zona marcada en el gráfico 10.2 y una probabilidad 0.99 de estar donde indica el gráfico 10.3. Concentremos nuestra atención en el caso del gráfico 10.2, correspondiente a la zona donde se halla el 95% de todas las medias muestrales posibles.

Se extrae la muestra (probabilística, con todos los resguardos que corresponda para que admita la generalización de las conclusiones a que lleve), en esa muestra calculamos \(\overline{x}_{obs}\). Supongamos que la muestra da lugar a la media que está indicada en el gráfico 10.4.

Figura 10.4: Ubicación de \(\overline{x}\).

Si construimos un intervalo de la misma amplitud que el anterior, pero ahora centrado en \(\overline{x}_{obs}\), en vez de centrado en \(\mu\), vemos en la figura 10.5 que ese intervalo contiene a \(\mu\).

Figura 10.5: Intervalo construido alrededor del valor observado de \(\overline{x}\) que contiene a \(\mu\)

Si la \(\overline{x}_{obs}\) fuera la que está en el gráfico 10.6.

Figura 10.6: Intervalo construido alrededor de \(\overline{x}_{obs}\) que contiene a \(\mu\)

También un intervalo alrededor de ella contendría a \(\mu\). Por el contrario en el caso de la figura 10.7:

Figura 10.7: Intervalo construido alrededor de \(\overline{x}_{obs}\) que NO contiene a \(\mu\)

El intervalo alrededor de \(\overline{x}_{obs}\) no contiene a la media poblacional.

• ¿Qué condición debe cumplir \(\overline{x}_{obs}\) para que el intervalo que se construya a su alrededor contenga a \(\mu\)?

  • Debe estar entre \(\mu - 1.96*\frac{\sigma}{\sqrt{n}}\) y \(\mu + 1.96*\frac{\sigma}{\sqrt{n}}\)

• ¿Qué proporción de las \(\overline{x}\) cumple esa condición?

  • El 95% de ellas.

Así, el 95% de las \(\overline{x}\) posibles dará lugar a intervalos que contengan a \(\mu\), el 5% restante de las \(\overline{x}\) producirá intervalos que no contienen a \(\mu\).

Es importante señalar que no sabemos si nuestro intervalo contiene a \(\mu\) o no, solo sabemos que hay una probabilidad de 0.95 que la contenga. Es decir, es muy probable que el intervalo contenga a \(\mu\), pero no es seguro.

¿Cuál es la expresión de ese intervalo?, dado que está centrado en \(\overline{x}_{obs}\), hay que sumar y restar a ese estimador lo mismo que sumamos y restamos a \(\mu\) para construir el intervalo anterior, por lo que resulta:

\[\overline{x}_{obs} - 1.96*\frac{\sigma}{\sqrt{n}}\ ;\ \overline{x}_{obs} + 1.96*\frac{\sigma}{\sqrt{n}}\]

Estos son dos números que constituyen los límites de un intervalo que tiene una probabilidad 0.95 de contener al parámetro \(\mu\). De manera equivalente decimos que, de cada 100 intervalos que se construyan con este procedimiento, 95 contendrán a la media de la población. O bien que el 95% de las muestras aleatorias de tamaño \(n\) que se extraigan de la población, proveerán valores de \(\overline{x}\) que conducirán a intervalos que contengan a la media de la población.

Cuando logramos construir un intervalo así decimos que se ha estimado a \(\mu\) con un 95% de confianza. El primero valor de los indicados se llama límite inferior (\(L_i\)) y el segundo, límite superior (\(L_s\)). Así entonces:

\[L_{i} = \overline{x}_{obs} - 1.96*\frac{\sigma}{\sqrt{n}}\]

\[L_{s} = \overline{x}_{obs} + 1.96*\frac{\sigma}{\sqrt{n}}\]

Podemos ahora mejorar la estimación puntual del ejemplo de quienes terminaron la carrera universitaria: encontramos que, en la muestra, la nota promedio con que egresan es de 6.50 (\(\overline{x}_{obs} = 6.50\)). Si se conoce que la desviación estándar de la población es de 0.8 (\(\sigma = 0.8\)), estimamos la nota promedio con que se egresa, reemplazando:

\[L_{i} = 6.50 - 1.96*\frac{0.8}{\sqrt{400}} = 6.42\ \]

\[L_{s} = 6.50 + 1.96*\frac{0.8}{\sqrt{400}} = 6.58\]

Leemos este resultado diciendo que tenemos un confianza del 95% que el intervalo \([6.42; 6.58]\) contiene a la media de las notas promedio que alcanzan quienes terminan la carrera. La confianza del 95% está incluida en la construcción del intervalo en el número 1.96 que multiplica al error estándar de \(\overline{x}\).

La notación general para los límites de este intervalo al 95% de confianza para la media puede abreviarse indicando de una sola vez ambos límites, si se escribe:

\[\overline{x}_{obs} \pm 1.96*\frac{\sigma}{\sqrt{n}}\]

Con lo que queremos indicar que a \(\overline{x}_{obs}\) se le suma y se le resta la expresión \(1.96*\frac{\sigma}{\sqrt{n}}\)

En el ejemplo, quedaría \(6.50 \pm 0.08\), que indica cuál es la media muestral (el estimador puntual) y la cantidad que debe sumarse y restarse para llegar a los límites.

Si quisiéramos estar más seguros de que el intervalo contiene a \(\mu\), podríamos usar los puntos que delimitan el \(99\%\) del área. Para ello, \(z\) vale \(2.57\) y los límites del intervalo resultan: \(\overline{x}_{obs} \pm 2.57*\frac{\sigma}{\sqrt{n}}\)

Para el ejemplo anterior, con una confianza del \(99\%\), el intervalo es:

\[L_{i} = 6.50 - 2.57*0.04 = 6.50 - 0.10 = 6.40\]

\[L_{s} = 6.50 + 2.57*0.04 = 6.50 + 0.10 = 6.60\]

Con lo que ahora diremos que, con una confianza del 99%, el intervalo \([6.40; 6.60]\) contiene a la media de las notas con que se egresa de esa carrera universitaria. Otra opción es la de escribir el intervalo como \(6.50 \pm 0.10\), la media muestral es la misma y aumentó lo que debe alejarse de ella para llegar a los límites.

Notemos que este aumento en la confianza de la estimación, al pasar del \(95\%\) al \(99\%\), tiene un costo, porque el intervalo es ahora más amplio: el límite inferior es menor que en el anterior y el superior, mayor. Antes el intervalo iba desde 6.42 hasta 6.58 y ahora va desde 6.40 hasta 6.60, el segundo intervalo empieza antes y termina después; es de mayor longitud. Más tarde volveremos sobre este punto.

De manera general, el intervalo se escribe como \(\overline{x}_{obs} \pm z*\frac{\sigma}{\sqrt{n}}\), dejando z como variable, que puede reemplazarse por el valor que corresponda según la confianza que se elija para la estimación (por ahora 1.96 para 95% y 2.57 para 99%)

Sin embargo, esta manera de calcular los límites del intervalo tiene un problema para usarse en la práctica, ya las fórmulas para calcular los límites, requieren que se conozca \(\sigma\), la desviación estándar de la población, pero como nuestros datos son muestrales, y no la conocemos. A cambio de ella usaremos como aproximación a la desviación estándar de la muestra, a la que sí podemos calcular con los datos disponibles⁶⁵. Con ese ajuste, la expresión para el cálculo de los límites del intervalo de confianza será:

\[\overline{x}_{obs} \pm z*\frac{s}{\sqrt{n}}\]

Que puede representarse gráficamente como en la figura 10.8:

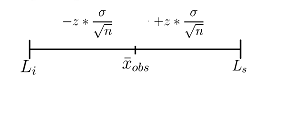
Figura 10.8: Estructura del intervalo de confianza

En este gráfico solo podemos dibujar el segmento que representa al intervalo en torno a \(\overline{x}_{obs}\), pero no podemos dibujar la campana correspondiente a la distribución, ya que no conocemos \(\mu\) que es donde la campana se centra.

Ejemplo (datos reales): Se dispone de una muestra de 277 estudiantes que rindieron el primer parcial de una asignatura, conocemos sus notas y queremos usarlas para hacer una estimación de la nota promedio de todo el curso (que cuenta con 1600 estudiantes). Haremos esa estimación con una confianza del 95%.

De la muestra hemos obtenido \(\overline{x}_{obs} = 6.63\) y \(s = 2.15\), con lo que los límites resultan:

\[\overline{x}_{obs} \pm z*\frac{s}{\sqrt{n}} = 6.63 \pm 1.96*\frac{2.15}{\sqrt{277}} = 6.63 \pm 1.96*0.13 = 6.63 \pm 0.25\]

Usando primero el signo menos, obtenemos \(L_i= 6.38\) y luego sumando \(L_s = 6.88\). Entonces podemos afirmar el intervalo \([6.38; 6.88\)] contiene a la nota promedio del total de estudiantes del curso, con una confianza del 95%.

Ejemplo (datos reales): Para estimar el ingreso salarial promedio del Gran Córdoba, se parte de los valores de media y desviación estándar que da la EPH: \(\overline{x}_{obs} = 14979.02\), \(s=9453.94\) y \(n=754\) para reemplazar:

\[\overline{x}_{obs} \pm z*\frac{s}{\sqrt{n}} = 14979.02 \pm 1.96*\frac{9453.94}{\sqrt{754}} = \] \[14979.02 \pm 1.96*344.29 = 14979.02 \pm 674.8\]

Así, hay una confianza de 95% que el intervalo \([14304.2, 15653.8]\) contenga al promedio de ingreso salarial de toda la población que trabaja en relación de dependencia y reside en el aglomerado Gran Córdoba, en el tercer trimestre de 2018.

Una representación gráfica de esta estimación es la siguiente:

Estimación de la media de ingresos. 95%

Para construir en intervalo con un nivel de confianza de 99%, reemplazamos el valor de \(z\) anterior de \(1.96\) por el de \(2.57\)

\[\overline{x} \pm z*\frac{s}{\sqrt{n}} = 14979.02 \pm 2.57*\frac{9453.94}{\sqrt{754}} = \] \[14979.02 \pm 2.57*344.29 = 14979.02 \pm 884.8\]

Ahora hay una confianza de 99% que el intervalo \([14094.2, 15863.8]\) contenga al parámetro que se está estimando. Comparada con la salida anterior, solo han cambiado los límites del intervalo, ya que son los mismos datos muestrales. El cambio en la confianza se realiza por un cambio en el valor de \(z\), los percentiles de la distribución normal y eso hace que cambien los límites. El gráfico tiene ahora la forma siguiente:

Estimación de la media de ingresos. 99%

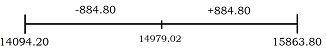
Se observa que un aumento en la confianza incide en la amplitud del intervalo, éste último es más amplio que el primero construido, los límites están más lejos uno de otro. Más adelante trataremos esta relación con detalle.

10.4 Estimación de la proporción

Cuando trabajamos con variables cualitativas (nominales u ordinales) no es posible calcular la media ni la desviación estándar sino solo considerar la proporción de casos que hay en una categoría que elegimos. La proporción es la frecuencia relativa de la categoría que se elige, la cantidad de casos en esa categoría dividida el tamaño de la muestra. Cuando se trata de variables con solo dos categorías (dicotómicas) puede elegirse cualquiera de ellas. Por ejemplo si es el resultado de un examen y las categorías son aprobado – no aprobado, podemos interesarnos por la proporción de cualquiera de ellas, ya que la otra es el complemento (lo que le falta para llegar a uno). Si una es 0.70 (70%), la otra no puede sino ser 0.30 (30%). Es diferente si la variable tiene más de dos categorías, por ejemplo si se trata de la intención de voto para las elecciones presidenciales. Allí es usual que haya más de dos partidos que aspiran a la presidencia, por lo que, conocer la proporción de uno de ellos no nos dice mucho sobre la de cada uno de los otros: si hay cinco partidos y uno se lleva el 40%, solo sabemos que el 60% restante se reparte entre los otros cuatro, pero no sabemos cuánto le corresponde a cada uno. A estos casos los trataremos como si fueran dicotómicos: una categoría será el partido que nos interesa y la otra categoría estará formada por todos los demás. Así, si un partido tiene una proporción de su favor, solo nos interesa que tiene una proporción de 0.60 que no está a su favor y no nos preocupamos por saber cómo se reparte ese 60% en los demás partidos. Tratamos una categoría frente a todas las demás. De este modo es que puede definirse la proporción de personas que usa anticonceptivos orales, frente a quienes usan todos los demás métodos; o la proporción de quienes promocionaron una asignatura frente a regulares y libres; o la proporción de quienes nacieron en Argentina entre el estudiantado de origen extranjero que hay en España, sin interesarnos por el modo en que se distribuye la proporción entre las demás nacionalidades. Lo que hacemos con este procedimiento es simplemente llamar la atención sobre una categoría y confrontarla con el resto indiscriminado. La categoría elegida o categoría de referencia, se llama éxito, su frecuencia absoluta, cantidad de éxitos y su frecuencia relativa proporción de éxitos.

Por este procedimiento trataremos siempre con dos grupos, uno formado por los casos que son de nuestro interés y el otro por los demás casos.

Existen varios procedimientos para construir intervalos de confianza para la proporción, aquí mencionaremos el de Clopper-Pearson, el de Wald y el de Wilson. Puede encontrarse una revisión más amplia en R. G. Newcombe (1998).

10.4.1 Intervalo de Clopper-Pearson

El primer modo para construir un intervalo para estimar la proporción, es usar la distribución binomial (Clopper and Pearson (1934)). Para ello, partimos del estimador puntual y buscamos los dos valores de \(\widehat{p}\) que delimiten el 95% central de la distribución.

Ejemplo (datos reales): a partir de la muestra de estudiantes que rindieron el parcial se busca estimar, al 95% de confianza, la proporción de quienes lo aprobaron.

Sabemos que, en la muestra de 277 casos, 255 lo aprobaron, en consecuencia la proporción muestral de parciales aprobados es⁶⁶, \(\widehat{p} = \frac{255}{277} = 0.920.\) Este es nuestro estimador puntual de la proporción de estudiantes que aprobaron para todo el curso. \[\widehat{p}_{obs}=0.92\] La variable aleatoria “número de éxitos que se obtiene en cada muestra”, que es \(\widehat{x}\), tiene una distribución binomial con \(n=277\) y \(p=255/277\), por lo tanto, los valores de \(\widehat{p}\) resultan \(\widehat{p}=\frac{\widehat{x}}{n}=\frac{\widehat{x}}{277}\).
Para determinar los límites, primero se buscan los valores de \(\widehat{x}\) que acumulan 2.5% (el percentil 2.5 o cuantil 0.025) y el 97.5% (percentil 97.5 o cuantil .975) de la distribución binomial (en lugar de 0.920, usamos el cociente de 255/277, así se evita la pérdida de decimales):

(P.025 <- qbinom(.025, 277, 255 / 277))

## [1] 246

(P.975 <- qbinom(.975, 277, 255 / 277))

## [1] 263

Y luego se los lleva a \(\widehat{p}\), dividiendo por 277. Con lo que los límites del intervalo para estimar \(P\) al 95% son estas cantidades de éxitos (\(\widehat{x}\)) divididas el tamaño de la muestra:

(Li <- round(P.025 / 277, 4))

## [1] 0.8881

(Ls <- round(P.975 / 277, 4))

## [1] 0.9495

Diremos entonces que, con una confianza del 95%, el intervalo \([88.81; 94.95]\)% contiene a la proporción de estudiantes que aprobaron, en toda la población.

Se puede solicitar de un solo paso, por medio de:

Li <- qbinom(.025, 277, 255 / 277) / 277
Ls <- qbinom(.975, 277, 255 / 277) / 277
100 * round(c(Li, Ls), 4)

## [1] 88.81 94.95

Para el problema de la confianza en los demás, con los datos de Latinobarómetro, la tabla muestra que de 19748 personas que respondieron, 2833 creen que se puede confiar en la mayoría de las personas; es decir que, en la muestra, el 14.3% acuerda con esa afirmación. Para extrapolar ese resultado a la población a la que representa la encuesta procedemos como recién. Sea ahora la confianza del 99% (cuantiles 0.005 y 0.995)

## [1] 13.71 14.84

Entonces, hay una confianza del 99% que el intervalo \([13.7; 14.8]\)% contenga a la proporción de quienes creen que en general se puede confiar en las personas, en la población a la que se refiere el estudio Latinobarómetro.

Esta forma de construir el intervalo de confianza para la proporción -de Clopper-Pearson-, es la más antigua, se la conoce también como “método exacto”, porque no apela a aproximaciones para calcular los límites, sino que usa la distribución que corresponde al experimento: la binomial.

10.4.2 Intervalo de Wald

Si se cumplen las condiciones para realizar una aproximación normal de la distribución binomial, el razonamiento que seguimos para la estimación de \(P\) será análogo al que seguimos para estimar \(\mu\). La aproximación normal aplicada a la construcción de intervalos para la proporción se conoce con este nombre en referencia a Wald (1939), pero la primera presentación data de Laplace (1812).
La estructura de los límites del intervalo de confianza es ahora:

\[L_{i} = \widehat{p}_{obs} - z*\sigma_{\widehat{p}}\]

\[L_{s} = \widehat{p}_{obs} + z*\sigma_{\widehat{p}}\]

En la que:

\(\widehat{p}_{obs}\) es la proporción de casos en la categoría que estimamos calculada sobre los datos de la muestra.

\(z\) asume el valor de \(1.96\) si vamos a estimar con una confianza del 95%, ó de \(2.57\) si queremos una confianza del 99%.

\(\sigma_{\widehat{p}}\) es la desviación estándar del estimador:

\[\sigma_{\widehat{p}} = \sqrt{\frac{P*(1 - P)}{n}}\]

Pero, tal como pasó con la estimación de \(\overline{x}\), en la que ignorábamos \(\sigma\) por tratarse de un valor poblacional, ahora desconocemos \(P\) (¡es exactamente lo que estamos tratando de estimar!), por lo que deberemos necesariamente reemplazarla por su estimador:\(\widehat{p}_{obs}\)⁶⁷. Resultará:

\[{\widehat{\sigma}}_{\widehat{p}} = \sqrt{\frac{\widehat{p}_{obs}*(1 - \widehat{p}_{obs})}{n}}\]

Y los límites del intervalo son:

\[\widehat{p}_{obs} \pm z\sqrt{\frac{\widehat{p}_{obs}*(1 - \widehat{p}_{obs})}{n}}\]

Ejemplo (datos reales): repetimos la estimación de la proporción de quienes aprobaron el parcial, ahora con la aproximación de Wald. Con los datos de antes, la proporción muestral es \(\widehat{p}_{obs} = \frac{255}{277} = 0.920\) Este es nuestro estimador puntual de la proporción de quienes aprobaron de todo el curso. Para hacer el intervalo, usamos la expresión anterior y resulta:

\[\widehat{p}_{obs} \pm z\sqrt{\frac{\widehat{p}_{obs}*(1 - \widehat{p}_{obs})}{n}} = 0.920 \pm 1.96*\sqrt{\frac{0.92*0.08}{277}} = 0.920 \pm 0.032\]

Cuando restamos, obtenemos el límite inferior del intervalo:

\[L_{i} = 0.920 - 0.032 = 0.892\]

y sumando:

\[L_{s} = 0.920 + 0.032 = 0.952\]

Si se escribe de manera abreviada, la expresión toma la forma:

\[L_{i} = 0.920 \pm 0.032\]

Con el valor explícito de la proporción muestral que es el estimador puntual de \(P\).

El resultado dice que hay una confianza del 95% que el intervalo \([89.2; 95.2]\)% contenga a la proporción de estudiantes que aprobó en toda la población. El intervalo difiere un poco del hallado con el método exacto, porque es una aproximación.

La aplicación de este mismo método aproximado a la pregunta de Latinobarómetro, da por resultado, con una confianza de 99%:

## [1] 13.70 14.83

Que casi no difiere de la aplicación del método exacto

Esta forma de construir el intervalo de confianza para P resulta de calidad aceptable si el producto \(n*\widehat{p}_{obs}*(1 - \widehat{p}_{obs})\) es mayor a 5, y mejor aun si ese resultado es mayor a 10. Sin embargo, Cepeda-Cuervo et al. (2008) señalan evidencia sobre la inadecuación de esta estimación aun cuando la condición se cumple. Por esta razón se limita el uso de este modo de calcular el intervalo cuando el número de observaciones en mayor a cien⁶⁸.

10.4.3 Intervalo de Wilson

Una mejora para la calidad de la estimación es propuesta por R. Newcombe and Merino Soto (2006), con un intervalo llamado de score o de Wilson (1927), cuyos límites son:

\[\widehat{p} \pm \frac{z}{n}*\sqrt{\frac{\left( \widehat{p}*\left( 1 - \widehat{p} \right) + \frac{z}{4*n} \right)}{n}}\]

Este intervalo no colapsa para \(\widehat{p} = 0\) ó \(\widehat{p} = 1\) y tiene mejor calidad que el de Wald, es conveniente optar por esta alternativa si se trata de pequeñas muestras o de valores de \(\widehat{p}\) próximos a cero o a uno. De todos modos, siempre es preferible utilizar la distribución binomial que es la adecuada para modelar el proceso.

10.5 La calidad de las estimaciones por intervalo

Intuitivamente, una estimación es de mejor calidad si es “ajustada”, es decir si el intervalo es pequeño. Por ejemplo, si estimamos la edad de una persona entre 28 y 30 años, tenemos una estimación de mejor calidad que si decimos que tiene entre 20 y 40 años. Eso es porque el primer intervalo es más pequeño, los límites están más cerca. La primera estimación nos da más información que la segunda, porque delimita el valor al que estima entre números más cercanos. En las estimaciones que hemos hecho hasta aquí, de la media y de la proporción (salvo el intervalo de Clopper-Pearson), hemos partido del estimador puntual (\(\overline{x}\) y \(\widehat{p}\)) y desde él sumamos y restamos la misma cantidad para obtener los límites del intervalo.

Esa cantidad que sumamos y restamos determina la amplitud del intervalo: cuanto más grande sea, tanto mayor será el intervalo, es decir, tanto mayor será la distancia entre los límites inferior y superior. Esa cantidad se denomina error de estimación. Las estimaciones están siempre acompañadas de un error, es un componente intrínseco al proceso. No es error en el sentido de equivocación o de falla, sino de imprecisión, una imprecisión que no puede evitarse, que no puede hacerse igual a cero. Se calcula como la distancia que hay desde el centro del intervalo hasta cualquiera de los límites. En el ejemplo anterior, sobre la estimación intuitiva de la edad de alguien, el centro del primer intervalo es 29, por lo que el error es 1 año, por eso se puede también escribir como \(29 \pm 1\). El segundo intervalo de este ejemplo tiene centro en 30 y el error es de 10 años, lo escribimos \(30 \pm 10\). Independientemente que el centro de los intervalos difiera levemente, este segundo intervalo tiene un mayor error de estimación. Esto es equivalente a decir que tiene menos precisión.

Se llama error de estimación a la distancia que hay entre el estimador puntual y cualquiera de los límites del intervalo. Cuanto mayor es el error de estimación menor es su precisión.

En la estimación del promedio con que se termina una carrera universitaria, escribimos \(6.50 \pm 0.08\) al estimar al 95% de confianza y \(6.50 \pm 0.10\) cuando la confianza se pasó al 99%. Allí estábamos escribiendo el intervalo como el estimador más/menos el error de estimación. En el primer caso el error de estimación es de 0.08 y en el segundo de 0.10, por eso decimos que la primera estimación es más precisa, tiene menos error. Con la estimación de los ingresos salariales sucedió lo mismo, al 95% el error 674.80 fue y al 99% subió a 884.80. Del mismo modo, al estimar, con una confianza del 95%, la proporción de quienes aprobaron el parcial escribimos \(0.920 \pm 0.032\), el error de estimación es en este caso de 0.032 (ó 3.2%). La estimación de la proporción de gente que cree que se puede confiar en los demas, hecha con el mismo nivel de confianza, arrojó un error de estimación de 0.0056, 0.56%.

10.5.1 El error de estimación en la media

En la expresión general de la estimación por intervalo de \(\mu\), el error es el término que se suma y resta: \(z*\frac{s}{\sqrt{n}}\). ¿De qué depende que ese término sea grande o chico?

Hay tres elementos en este término: \(z\), \(s\) y \(n\). De ellos va a depender que haya más o menos error en la estimación o, dicho de otra manera, que la estimación sea más o menos precisa. Veamos el efecto de cada uno:

• \(z\): Es elegido por el equipo de investigación cuando se establece la confianza. En los ejemplos que hemos visto, asumió el valor de 1.96 para un 95% de confianza o de 2.57 para una confianza de 99%. Cuanto más confianza o certeza queramos tener en nuestra estimación, más grande será \(z\) y, en consecuencia mayor será el error de estimación. Por lo tanto no se pueden tener las dos cosas: más confianza va acompañada de menos precisión. Si todos los demás elementos del error quedan fijos, los intervalos más amplios proveen menos información, pero mayor certeza en la inclusión del parámetro que se estima. Para elegir el nivel de confianza (y en consecuencia determinar \(z\)) debe tomarse una decisión que equilibre la confianza y la precisión, ya que si una crece la otra disminuye. Si alguien intentara lograr precisión absoluta, es decir, error igual a cero, encontraría una confianza también igual a cero, es decir, ninguna certeza. A la inversa, intentar fijar la confianza en el 100%, lleva a un error infinito.

• \(s\): La desviación estándar en la muestra. Es la medida de la variabilidad de los datos que se observan, y es una estimación de la verdadera variabilidad que tiene la característica que estamos estudiando en la población. Incide negativamente sobre el error, cuanto más grande es \(s\) más error tenemos. Eso refleja el hecho que si la población es muy heterogénea respecto de la cualidad que queremos estimar, tendremos estimaciones de peor calidad que si es similar para los individuos de la población. Sobre \(s\) no podemos decidir, no tenemos control sobre su valor, si es grande, tendremos peores estimaciones que si es pequeña. El muestreo estratificado es una forma de enfrentar situaciones de mucha dispersión, construyendo subconjuntos (estratos) que contengan elementos homogéneos en su interior, es decir que tengan menos dispersión que el conjunto completo.

• \(n\): El tamaño de la muestra, se encuentra en el denominador del término del error, por lo que su aumento reduce el error. Cuanto más grande sea \(n\), menor será el error, es decir que muestras de mayor tamaño dan mayor precisión. En principio, podemos elegir \(n\), pero depende del presupuesto que se prevea para la investigación. Si se puede obtener una muestra grande siempre es preferible, porque se lograrán estimaciones con menos error, de mejor calidad.

Esto no debe confundirse con la calidad de la muestra. Todo lo mencionado sobre estimación, supone que se trata de muestras probabilísticas, es decir muestras aleatorias, para las cuales rigen las leyes de probabilidad que hemos usado. Si la muestra no es aleatoria, no se pueden hacer estimaciones con estos procedimientos y; esto es muy importante: no se mejora una muestra tomando más casos. Si la muestra no es probabilística, la estimación no mejorará porque se tomen muchos casos.

La distribución \(t\) de Student tiene aplicación cuando se trata de muestras pequeñas, sin embargo, como se señaló antes, cuando los grados de libertad aumentan, esta distribución se aproxima a la normal. Por esta razón, al construir los intervalos, no hay inconveniente en calcular los percentiles que corresponden al nivel de confianza elegido, usando el modelo \(t\). Si la muestra es suficientemente grande, el resultado será el mismo que con la normal. Así se evita decidir cada vez, en base al tamaño de la muestra, si se usa una distribución o la otra. Por esa razón, de aquí en adelante, calcularemos los percentiles necesarios para estimar la media, con la distribución \(t\) con \(n-1\) grados de libertad.

Para ejemplificar los efectos de los diferentes elementos en el error de estimación, usaremos la base de la Encuesta Nacional sobre Prevalencias de Consumo de Sustancias Psicoactivas 2011. Con esos datos, estimaremos la edad promedio a la que las personaslos encuestadas dicen que tomaron alcohol por primera vez en su vida. La variable se llama BIBA03 y corresponde a la siguiente pregunta del cuestionario:

¿Qué edad tenía cuando consumió bebidas alcohólicas por primera vez? (Edad en años) Cuya descripción es la siguiente:

medida	valor
media	18.07
mediana	17.00
desviación estándar	4.71
n	24949.00

10.5.1.1 Efecto de la confianza sobre el error

Para el cálculo de los límites del intervalo, usamos media, desviación, tamaño de muestra y, para una confianza de 90% usamos los cuantiles 0.05 y 0.95 de la distribución \(t\) con 24948 grados de libertad (que no difiere de la normal)

Li_90 <- mean(enprecosp$BIBA03) +
  qt(.05, 24948) * sd(enprecosp$BIBA03) /
    sqrt(length(enprecosp$BIBA03))

Ls_90 <- mean(enprecosp$BIBA03) +
  qt(.95, 24948) * sd(enprecosp$BIBA03) /
    sqrt(length(enprecosp$BIBA03))

round(c(Li_90, Ls_90), 2)

## [1] 18.02 18.12

El error es de:

round((Ls_90 - Li_90) / 2, 3)

## [1] 0.049

Variamos el nivel de confianza, primero al 95%:

Li_95 <- mean(enprecosp$BIBA03) +
  qt(.025, 24948) * sd(enprecosp$BIBA03) /
    sqrt(length(enprecosp$BIBA03))

Ls_95 <- mean(enprecosp$BIBA03) +
  qt(.975, 24948) * sd(enprecosp$BIBA03) /
    sqrt(length(enprecosp$BIBA03))

round(c(Li_95, Ls_95), 2)

## [1] 18.01 18.13

Con un error de estimación:

round((Ls_95 - Li_95) / 2, 3)

## [1] 0.058

Y luego al 99%

Li_99 <- mean(enprecosp$BIBA03) +
  qt(.005, 24948) * sd(enprecosp$BIBA03) /
    sqrt(length(enprecosp$BIBA03))

Ls_99 <- mean(enprecosp$BIBA03) +
  qt(.995, 24948) * sd(enprecosp$BIBA03) /
    sqrt(length(enprecosp$BIBA03))

round(c(Li_99, Ls_99), 2)

## [1] 17.99 18.15

que lleva el error de estimación a:

round((Ls_99 - Li_99) / 2, 3)

## [1] 0.077

Estas tres primeras estimaciones muestran cómo, sin cambiar el tamaño de la muestra ni la dispersión, el error aumenta (los intervalos se vuelven más amplios) cuando crece la confianza.

10.5.1.2 Efecto del tamaño de la muestra sobre el error

Ahora se seleccionan solo las respuestas dadas por mujeres, con lo que la descripción de la variable es:

medida	valor
media	18.97
mediana	18.00
desviación estándar	5.47
n	12196.00

El total de casos es de 12196, al construir el intervalo al 90%

## [1] 18.89 19.05

Cuyo error es:

## [1] 0.081

Bastante más grande que el que se obtuvo al mismo nivel de confianza, para la muestra completa.

10.5.2 El error de estimación en la proporción

En la construcción del intervalo de Wald, el término del error en la estimación de la proporción es:

\[z*\sqrt{\frac{\widehat{p}*\left( 1 - \widehat{p} \right)}{n}}\]

En él hay dos elementos en común con el error en la estimación de la media: los valores de \(z\) y de \(n\). No agregaremos nada sobre ellos, porque el efecto es el mismo que en la media: un aumento de \(z\) por aumento de la confianza, da lugar a un incremento en el error de estimación, mientras que un aumento en el tamaño de la muestra, lo reduce.

Lo nuevo en este caso es que no hay \(s\), por el contrario, lo que hay en su lugar es el producto de la proporción por su complemento \(\widehat{p}*\left( 1 - \widehat{p} \right)\), que se encuentra afectado por la raíz, pero eso no interesa para analizar su efecto sobre la precisión.

Recordemos el problema de la medición de la dispersión para variables nominales. Se vio que una variable nominal tiene poca dispersión cuando una categoría “absorbe” a las otras, cuando muchos casos están en una sola categoría, o cuando una categoría tiene una frecuencia superior a todas las demás. Por el contrario, la dispersión es elevada cuando las frecuencias son similares, cuando la distribución de casos es “pareja” en todas las categorías. En la estimación de la proporción estamos tratando solo con dos categorías, por lo que la dispersión será máxima cuando las proporciones de ellas sean similares. Siendo solo dos, son iguales cuando cada una de ellas vale \(0.50\) (\(\widehat{p} = 0.50\) y \((1 - \widehat{p}) = 0.50\)), porque la mitad de los casos está en cada categoría. Por el contrario, la dispersión será menor cuanto más concentrados estén los casos en una de las categorías. Si, por ejemplo la proporción es \(0.10\) \((\widehat{p} = 0.10\) y \(( 1 - \widehat{p}) = 0.90)\) tendremos concentración de casos en una categoría, es decir, poca dispersión. Eso está expresado en la variabilidad medida como el producto de \(\widehat{p}\) por su complemento: \(\widehat{p}*(1 - \widehat{p})\)

Cuando \(\widehat{p} = 0.50\) y \(( 1 - \widehat{p}) = 0.50\), entonces, el producto \(\widehat{p}*(1 - \widehat{p}) = 0.25\). Por el contrario, cuando \(\widehat{p} = 0.10\) y \(( 1 - \widehat{p}) = 0.90\), entonces, el producto \(\widehat{p}*( 1 - \widehat{p}) = 0.09\).

Por eso, el producto \(\widehat{p}*( 1 - \widehat{p})\) es una medida de la dispersión de la variable nominal y ocupa, dentro del término del error, un lugar equivalente al de la varianza en la estimación de la media.

¿Cómo incide esto en el error de estimación? Como con la media, cuando la dispersión es grande, el error también lo es, entonces el error será mayor cuanto más parecidas sean \(\widehat{p}\) y \((1 - \widehat{p})\), dicho de otra manera, cuando \(\widehat{p}\) sea cercana a 0.50.

El razonamiento es el mismo que con la media, cuanto mayor sea la dispersión tanto más grande será el error y menos precisa la estimación. Pero en el caso de la media, la dispersión está medida con la desviación estándar, mientras que en la proporción, viene dada por el producto \(\widehat{p}*( 1 - \widehat{p})\), que es máximo cuando \(\widehat{p}\) es cercano a 0.50. Entonces, las peores condiciones para hacer una estimación de la proporción, serán aquellas en que la característica que se estima afecta a porciones cercanas a la mitad de la muestra, allí será máxima la dispersión y en consecuencia también el error de estimación.

Ejemplo (datos ficticios): a partir de una encuesta, se estima la proporción de votos que tendrá un partido político en las próximas elecciones. La muestra es de 400 casos y 90 personas dijeron que votarán a ese partido. Como 90 es el 22.5% de 400 (su frecuencia relativa), esa es la proporción muestral \(\widehat{p}_{obs}=0.225\) y la estimación por intervalo al 95% de confianza da:

\[\widehat{p}_{obs} \pm z*\sqrt{\frac{\widehat{p}_{obs}*(1 - \widehat{p}_{obs})}{n}} = 0.225 \pm 1.96*\sqrt{\frac{0.225*(1 - 0.225)}{400}} = 0.225 \pm 0.041\]

Los límites del intervalo son \(L_i = 0.1841\) y \(L_s = 0.2659\). Para comunicarlo, diremos que ese partido político tiene una intención de voto de entre el 18.41% y el 26.59%. Aunque la lectura correcta es que hay una confianza del 95% que el intervalo \([18.41; 26.59]\)% contenga a la verdadera proporción de personas que dicen que votarán por ese partido.

Repitamos el ejercicio, ahora suponiendo que la cantidad de personas que dice que lo votaría son 200 de los 400 encuestados, es decir si la proporción muestral hubiese sido del 50%. Siempre al 95% de confianza, la estimación es:

\[\widehat{p}_{obs} \pm z*\sqrt{\frac{\widehat{p}_{obs}*(1 - \widehat{p}_{obs})}{n}} = 0.50 \pm 1.96*\sqrt{\frac{0.50*(1 - 0.50)}{400}} = 0.50 \pm 0.049\]

Vemos que el error de estimación ha pasado de 4.1% en el anterior a 4.9% ahora, sin que hayamos cambiado la confianza ni el tamaño de la muestra. Ese es el efecto de la proporción cuando es cercana al 50%.

Ejemplo (datos reales): Sobre la misma encuesta anterior, se estima la proproción de personas que dicen haber bebido alguna vez en su vida. La pregunta se llama BIBA01 y está formulada: ¿Ha consumido alguna bebida alcohólica, como por ejemplo vino, cerveza, whisky o similares, alguna vez en la vida? 1 Sí 2 No 9 Ns/nc

La tabla de distribución de frecuencias genera:

¿Ha consumido alguna bebida alcohólica, como por ejemplo vino, cerveza, whisky o similares, alguna vez en la vida?	\(f\)
Sí	25709
No	8621
Ns/nc	13
Sum	34343

Cuando se consideran solo los casos válidos, la tabla queda:

¿Ha consumido alguna bebida alcohólica, como por ejemplo vino, cerveza, whisky o similares, alguna vez en la vida?	\(f\)
Sí	25709
No	8621
Sum	34330

A nivel de la muestra, quienes contestan que han bebido alguna vez son el \(74.9\)% (\(25709/34330\)). Extendemos ese resultado a la población construyendo un intervalo de Clopper-Pearson al 95% y expresando el resultado en porcentajes:

Li_prop_biba1_95 <- qbinom(.025, 34330, 25709 / 34330) / 34330
Ls_prop_biba1_95 <- qbinom(.975, 34330, 25709 / 34330) / 34330
100 * round(c(Li_prop_biba1_95, Ls_prop_biba1_95), 4)

## [1] 74.43 75.35

El error de estimación es 0.92% y, si aumenta la confianza al 99%:

Li_prop_biba1_99 <- qbinom(.005, 34330, 25709 / 34330) / 34330
Ls_prop_biba1_99 <- qbinom(.995, 34330, 25709 / 34330) / 34330
100 * round(c(Li_prop_biba1_99, Ls_prop_biba1_99), 4)

## [1] 74.28 75.49

Con un error de 1.2

Vemos que al aumentar el nivel de confianza se reduce la precisión, ya que los límites se distancian, volviendo más amplio al intervalo, aumentando el error de estimación.

10.6 Probabilidad de cobertura

Un elemento adicional a considerar para la correcta interpretación de las estimaciones por intervalo, es la probabilidad de cobertura, que indica la probabilidad que tienen los límites de contener efectivamente al parámetro. En el caso de la media, se escribe \(P(L_{i}\leq \mu \leq L_{s})\) y para la proporción, se escribe como \(P(L_{i} \leq P \leq L_{s})\) en la que \(L_i\) y \(L_s\) son variables aleatorias que corresponden a los límites del intervalo. Esta probabilidad de cobertura puede ser igual, menor o mayor que la confianza, que es una cobertura nominal, es decir, la que predice la teoría. La probabilidad de cobertura es práctica, se calcula de manera empírica, por simulación.

Para el caso de la estimación de la proporción, Cepeda-Cuervo et al. (2008) muestran que el intervalo de Clopper-Pearson tiene una probabilidad de cobertura que supera a la nominal para todos los tamaños de muestra, por eso se lo considera conservador; ya que ofrece más certidumbre que la que se declara en la confianza. Al contrario, el intervalo de Wald muestra probabilidad de cobertura inferior a la nominal aun cuando se usen muestras grandes. El intervalo de Wilson ofrece una probabilidad de cobertura más cercana a la nominal que el de Wald y que el exacto.

En el sitio https://istats.shinyapps.io/ExploreCoverage/ se pueden hacer simulaciones para diferentes valores de proporción poblacional, confianza, tamaño de muestra y cantidad de muestras. Cada muestra aleatoria genera un intervalo de confianza y se observa si éste incluye o no al valor poblacional. La figura 10.9 muestra una simulación que consiste en extraer 100 muestras de tamaño 50 de una población en la que la proporción vale \(0.30\) y construir un intervalo de confianza al \(95\%\) de confianza para cada una de ellas. La teoría predice que el \(95\%\) de los intervalos incluirá al valor \(P=0.30\), pero de los 100, 93 lo hacen (los verdes aciertan, los rojos no). Así, la probabilidad de cobertura es de 93%, que es menor que la nominal.

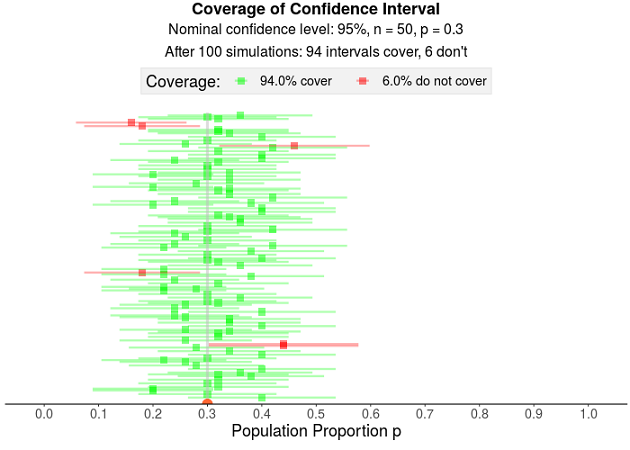
Figura 10.9: Simulación para el cálculo de la probabilidad de cobertura

En este capítulo hemos puesto en juego lo visto en los anteriores para poder generalizar las observaciones muestrales a toda la población de referencia, vemos que el modo con el que se hace es a través de los intervalos de confianza, que formalizan una práctica a la que estamos acostumbrados cuando hacemos estimaciones sobre cantidades que desconocemos: indicamos entre qué valores es más probable hallarlas.

La estructura general de los intervalos es:

\[estimador \pm error\ de\ estimacion\]

Esa expresión ha tomado diferentes formas, ya sea para estimar la media de variables cuantitativas o la proporción de éxitos, para la que hay varios procedimientos de obtención de los límites.

En cualquiera de los casos, la lectura del intervalo obtenido se expresa:

Hay una confianza \(1 - \alpha\) que el intervalo obtenido contenga al parámetro.

10.7 Hacerlo en R

La construcción de intervalos puede realizarse aplicando los procedimientos descriptos en el capítulo y dependiendo de cuál sea el origen de los datos.

10.7.1 Intervalo para la media

Para el ejemplo de los ingresos salariales (PP08D1), tomamos un subconjunto de la base eph.3.18 que contiene solo personas que declaran ingresos salariales no nulos.

asalariades_cba <- subset(eph.3.18, eph.3.18$PP08D1 > 0 & eph.3.18$AGLOMERADO == 13)

Recordemos que \(n\), el tamaño de la muestra, es la longitud (length) del vector que corresponde a esa variable. Sobre PP08D1, se construye el intervalo de manera directa, teniendo en cuenta que los valores -1.96 y 1.96 provienen de las probabillidades acumuladas de 0.025 y 0.975, que son las que delimitan la probabilidad 0.95 central. De modo que esos dos valores que estamos escribiendo “de memoria”, pueden pedirse al momento de construir los límites del intervalo. Además, por la razón que mencionamos antes, usamos la distribución \(t\) con \(n-1\) grados de libertad en todos los casos, ya que cuando la muestra es grande su valor coincide con el de la normal. Llamamos Li95 y Ls95 a esos límites y resulta:

Li95 <- mean(asalariades_cba$PP08D1) +
  qt(.025, 753) * sd(asalariades_cba$PP08D1) /
    sqrt(length(asalariades_cba$PP08D1))
Li95

## [1] 14303.13

Ls95 <- mean(asalariades_cba$PP08D1) +
  qt(.975, 753) * sd(asalariades_cba$PP08D1) /
    sqrt(length(asalariades_cba$PP08D1))
Ls95

## [1] 15654.9

• Límite inferior= 1.43031^{4}
• Límite superior= 1.56549^{4}

Observemos que las dos veces sumamos, el signo viene automático, porque el percentil 2.5 de \(z\) es negativo y el 97.5 positivo. Para escribirlo más compacto calculamos la media por un lado y el error de estimación, por otro:

mean(asalariades_cba$PP08D1)

## [1] 14979.02

qt(.025, 753) * sd(asalariades_cba$PP08D1) /
  sqrt(length(asalariades_cba$PP08D1))

## [1] -675.8864

qt(.975, 753) * sd(asalariades_cba$PP08D1) /
  sqrt(length(asalariades_cba$PP08D1))

## [1] 675.8864

Las dos operaciones dan el mismo valor absoluto, con el signo opuesto, entonces el resultado de la estimación se escribe: \[14979 \pm 675\]

Para construir en intervalo con un nivel de confianza de 99%, usamos los cuantiles 0.005 y 0.995 de la distribución \(t\) con 753 grados de libertad y llamamos Li99 y Ls99 a los límites:

Li99 <- mean(asalariades_cba$PP08D1) +
  qt(.005, 753) * sd(asalariades_cba$PP08D1) /
    sqrt(length(asalariades_cba$PP08D1))
Li99

## [1] 14089.93

Ls99 <- mean(asalariades_cba$PP08D1) +
  qt(.995, 753) * sd(asalariades_cba$PP08D1) /
    sqrt(length(asalariades_cba$PP08D1))
Ls99

## [1] 15868.11

• Límite inferior= 1.40899^{4}
• Límite superior= 1.58681^{4}

Nuevamente para la notación abreviada, como la media es la misma y sabemos que lo que se suma es lo mismo que lo que se resta, solo calculamos:

qt(.995, 753) * sd(asalariades_cba$PP08D1) /
  sqrt(length(asalariades_cba$PP08D1))

## [1] 889.0909

Y la estimación se escribe:\[14979 \pm 889\]

10.7.2 Intervalo para la proporción

Para estimar la propoción de personas inactivas a partir de la base de la EPH, hay que definir a esa categoría como la de referencia (1) en la variable “ESTADO” y asignar cero a las demás categorias. Para hacerlo, definimos “inactives”, como una nueva variable de la base eph.3.18 cuyo valor dependerá del que tenga “ESTADO”. Si “ESTADO” vale:

• 3 (inactivo), entonces “inactives” vale 1
• 0 o 4, “inactives” no se cuenta, porque son entrevistas no realizadas, o menores de 10 años, corresponde NA
• 1 o 2 “inactives” vale cero

eph.3.18$inactives <- ifelse(
  eph.3.18$ESTADO == 3, 1, ifelse(
    eph.3.18$ESTADO == 0 | eph.3.18$ESTADO == 4, NA, 0
  )
)

Y con una tabla verificamos que el 1 de la nueva variable corresponda al 3 de “ESTADO” y que todos los demás valores de “ESTADO” tengan asociado un cero en “activos”.

addmargins(table(eph.3.18$ESTADO, eph.3.18$inactives))

##      
##           0     1   Sum
##   0       0     0     0
##   1   23398     0 23398
##   2    1870     0  1870
##   3       0 23167 23167
##   4       0     0     0
##   Sum 25268 23167 48435

La nueva variable (inactives) tiene 25268 casos en el valor cero, que corresponden a 23398 a ESTADO = 1 (ocupados) más 1870 de ESTADO = 2 (desocupado) y 23167 casos en el valos uno, que son los 23167 de ESTADO = 3 (inactivo). El total de casos es ahora 48435, porque se quitaron los ceros y los cuatros.
Ahora la estimación al 95% de la proporción poblacional de personas inactivas, por método de Clopper-Pearson requiere que calculemos los cuantiles .025 y .975 de la distribución binomial con \(n=48435\) y \(p=23167/48435=0.478=47.8\%\) y que los dividamos por el tamaño de la muestra.

Li <- qbinom(.025, 48435, .478) / 48435
Ls <- qbinom(.975, 48435, .478) / 48435
round(c(Li, Ls), 4) * 100

## [1] 47.35 48.24

Si tenemos en cuenta que es una muestra grande, puede usarse el método de Wald, con \(\widehat{p}=0.478\) con el que los límites resultan:

Li <- .478 + qnorm(.025) * sqrt(.478 * (1 - .478) /
  48435)
Ls <- .478 + qnorm(.975) * sqrt(.478 * (1 - .478) /
  48435)
round(c(Li, Ls), 4) * 100

## [1] 47.36 48.24

Efectivamente, con un tamaño de muestra grande, el método de Wald, que usa la distribución normal como aproximación a la binomial da un resultado casi idéntico.

10.7.3 Cobertura

Los siguientes comandos generan 200 intervalos para estimar la media de ingresos salariales de la EPH a partir de 200 muestras, de tamaño 30. Es una simulación, porque se trata a los datos de la EPH como si fuera una población y a la media de los ingresos saariales de la EPH como si fuera el parámetro poblacional. El ejercicio sirve para observar el efecto, por ejemplo del tamaño de la muestra. La sintaxis dice lo siguiente:

• Se definen:
  • resultado: una matriz de datos
  • mu: la media de PP08D1 en la base asalariados_cba
  • N: la cantidad de casos en la población
  • n: tamaño de las muestras

resultado <- data.frame()
mu <- mean(asalariados_cba$PP08D1, na.rm = TRUE)
N <- length(asalariados_cba$PP08D1)
n <- 30

• Se repite 200 veces (cantidad de muestras, cada repetición produce una diferente)
• Se llama x el vector que contiene n números aleatorios (tamaño de cada muestra) provenientes de una distribución uniforme, entre 1 y N (que es el total de casos válidos), redondeado, sin decimales (0)
• Se llama muestra a n observaciones (aleatorias, que corresponde a los casos del vector x) de la columna 95, que es el lugar que ocupa la variable PP08D1
• A cada una de las 200 veces que repite, se define la columna 1 de resultado como el límite inferior del intervalo (a la media se suma el cuantil 0.025 por el error estándar)
• La segunda columna de resultado es el límite superior (se suma el cuantil 0.975)
• La tercera columna vale si si:
  • La primera columna (límite inferior) es menor que la media poblacional y al mismo tiempo, la segunda columna es mayor que ella; es decir si el intervalo contiene al parámetro.
  • Y vale no en caso contrario

for (i in 1:200) {
  x <- round(runif(n, 1, N), 0)
  muestra <- asalariados_cba[x, 95]
  resultado[i, 1] <- round(mean(muestra, na.rm = TRUE) +
    qt(.025, 29) * sd(muestra, na.rm = TRUE) / sqrt(length(muestra)), 1)
  resultado[i, 2] <- round(mean(muestra, na.rm = TRUE) +
    qt(.975, 29) * sd(muestra, na.rm = TRUE) / sqrt(length(muestra)), 1)
  resultado[i, 3] <- ifelse(
    resultado[i, 1] <= mu & resultado[i, 2] >= mu, "si", "no"
  )
}

Finalmente se pone nombre a las columnas de resultado:

names(resultado) <- c("Límite_inferior", "Límite_superior", "contiene_al_parametro")

La matriz puede visualizarse, desde el panel superior derecho o verse sus primeras filas:

##   Límite_inferior Límite_superior contiene_al_parametro
## 1         13282.4         20990.9                    si
## 2          9979.1         17119.6                    si
## 3         11920.1         17833.3                    si
## 4          8808.0         17592.0                    si
## 5         14672.3         23047.7                    si
## 6         16968.9         25897.7                    no

Y resumirse en una distridición de frecuencias:

(tabla_cobertura <- freq(resultado$contiene_al_parametro, report.nas = FALSE, cumul = FALSE))

## Frequencies  
## resultado$contiene_al_parametro  
## Type: Character  
## 
##               Freq        %
## ----------- ------ --------
##          no     13     6.50
##          si    187    93.50
##       Total    200   100.00

En este caso, la cobertura real es de 93.5%. Cada vez que se ejecute esta sintaxis se obtendrán resultados diferentes.

References

Cepeda-Cuervo, Edilberto, Wilson Aguilar, Víctor Cervantes, Martha Corrales, Iván Díaz, and Diana Rodríguez. 2008. “Intervalos de confianza e intervalos de credibilidad para una proporción.” Revista Colombiana de Estadistica 31 (2): 211–28.

Clopper, C. J., and E. S. Pearson. 1934. “The use of confidence or fiducial limits illistrated in the case of the binomial.” Biometrika 26 (4): 404–13. https://doi.org/10.1093/biomet/26.4.404.

Laplace, Pierre Simon Compte de. 1812. Théorie analytique des probabilités.

Newcombe, Robert G. 1998. “Two-Sided Confidence Intervals for the Single Proportion: Comparison of Seven Methods.” Statistics in Medicine 17 (8): 857–72. https://doi.org/10.1002/(SICI)1097-0258(19980430)17:8<857::AID-SIM777>3.0.CO;2-E.

Newcombe, Robert, and Cesar Merino Soto. 2006. “Intervalos de confianza para las estimaciones de proporciones y las diferencias entre ellas.” INTERDISCIPLINARIA 23 (2): 141–54.

Wald, Abraham. 1939. “Contributions to the Theory of Statistical Estimation and Testing Hypotheses.” The Annals of Mathematical Statistics 10 (4): 299–326. https://doi.org/10.1214/aoms/1177732144.

Wilson, Edwin B. 1927. “Probable Inference, the Law of Succession, and Statistical Inference.” Journal of the American Statistical Association 22 (158): 209–12. https://doi.org/10.1080/01621459.1927.10502953.

---

65. Esto es válido en la medida que se trate de muestras grandes (\(n > 30\)), en caso contrario, la distribución que debemos usar es la t de Student. Cuando fijemos la confianza, ya no serán z los valores que multiplicarán a \(\frac{\sigma}{\sqrt{n}}\) sino puntajes t, cuyos grados de libertad se calculan como \(n-1\). Pero, para poder usar la distribución t, los valores de la muestra deben provenir de una distribución normal en la población. Si esto no se cumple, la estimación puede realizarse buscando los límites a partir de una reconstrucción de la distribución empírica, por un método de remuestreo llamado “bootstrap”.↩︎

66. Como antes hicimos reemplazando a \(\sigma\) por \(s\).↩︎

67. Pero si \(\widehat{p}\) es muy pequeño, el límite inferior es negativo y si \(\widehat{p}\) es muy cercano a uno, el límite superior puede superar a 1, decimos que en estos casos el intervalo colapsa.↩︎